Contexte
Dans le cadre de mes études en classe préparatoire aux grandes écoles, je devais réaliser un travail d'initiative personnelle encadré qui constitue une épreuve des oraux. J'ai réalisé ce travail en binôme durant l'intégralité de ma seconde année de CPGE.
Notre TIPE portait donc sur l'étude des effets des balles aux tennis de table afin d'expliquer l'impact de la rotation de la balle sur sa trajectoire et les utilités d'un tel effet. Notre objectif était donc de réaliser une étude théorique du phénomène, puis de déterminer expérimentallement les coefficients caractéristiques des forces s'exerçant sur la balle en rotation.
Problématique du TIPE : Quelles sont les forces influençant la trajectoires des balles au tennis de table et comment déterminer la valeur de leurs coefficients caractéristiques ?
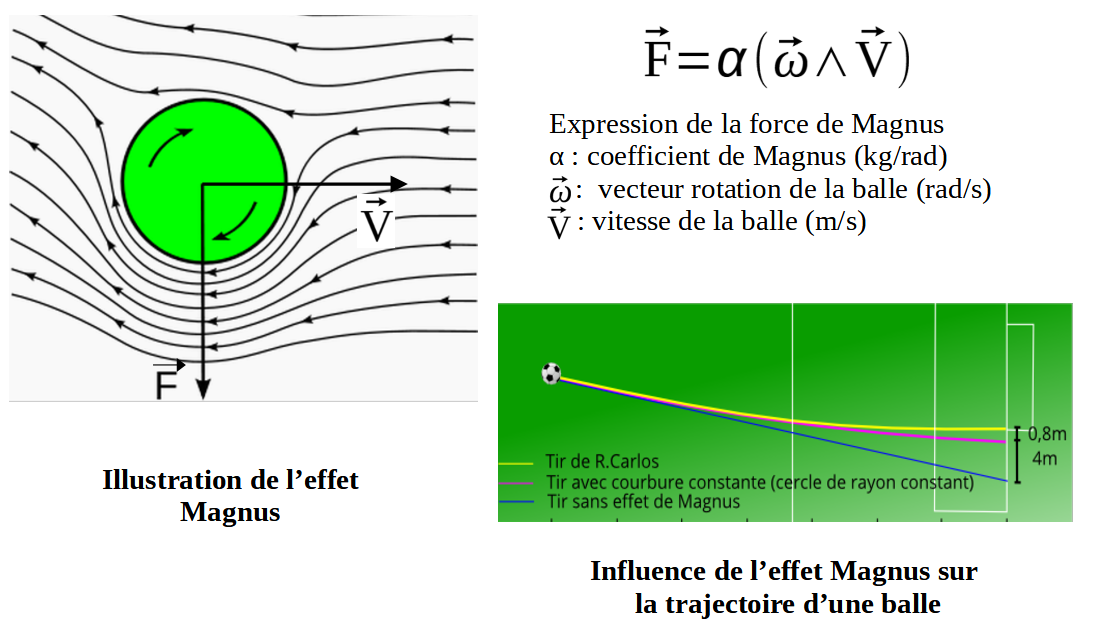
Effet Magnus
Lorsque la balle est mise en rotation dans l'air, le flux d'air va être accéléré d'un côté de la balle et ralenti de l'autre. Cela crée ainsi une différence de pression des 2 côtés de la balle, et donc une force : c'est l'effet Magnus

Force de traînée
L'air dans lequel se déplace la balle va freiner celle-ci en frottant sur sa surface. Cette force ainsi crée est proportionnelle au carré de la vitesse de la balle par rapport à l'air dans le cas d'un écoulement turbulent. Une force de portance est aussi présente, mais dans le cas d'une sphère comme ici, elle peut être négligée.
La force de frottement est régie par un coefficient de frottement qui varie selon l'objet étudié. C'est ce coefficient que nous avons cherché à déterminer.

Détermination du coefficient de frottement
Pour déterminer le coefficient de frottement, nous avons attaché la balle à une ficelle dans la soufflerie de notre lycée. En faisant passer de l'air dans la soufflerie, la balle se soulève grâce à la force de frottement, et nous pouvons mesurer l'angle formé par la ficelle avec la verticale lorsque la balle est à l'équilibre.
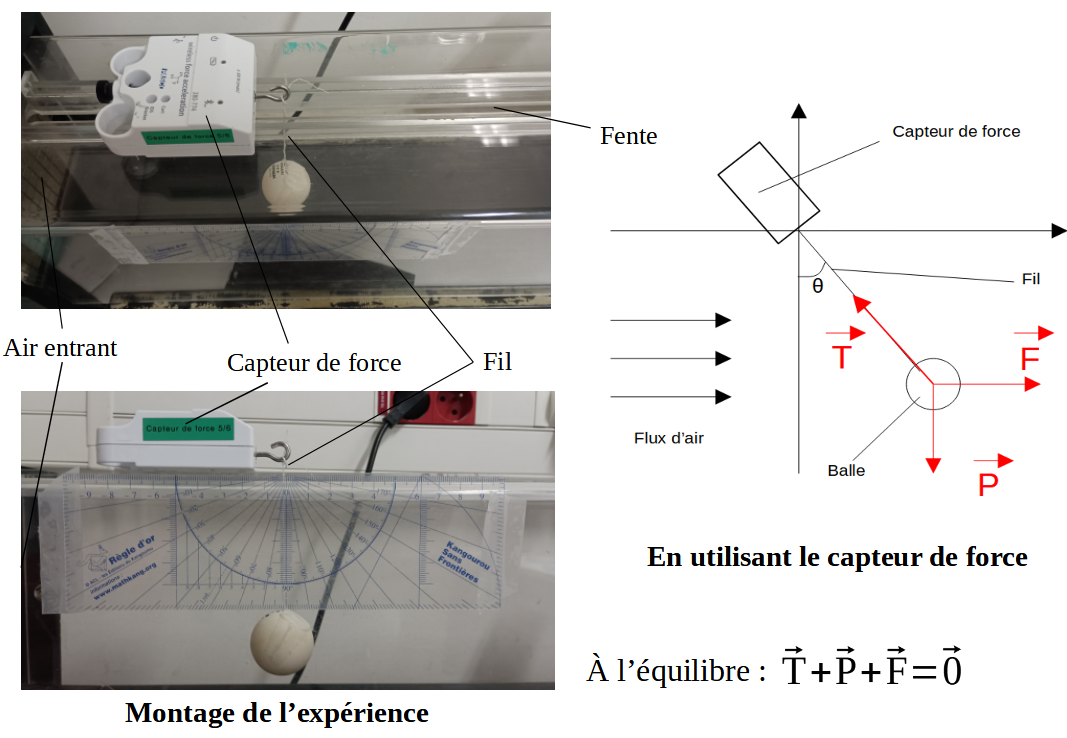
Avec une simple application du PFD, on peut alors déterminer la valeur du coefficient de frottement car on connait la valeur du poids et de la tension de la ficelle grâce à un capteur de force.
On obtient une valeur de 0,4 ce qui correspond aux valeurs trouvées dans la littérature.
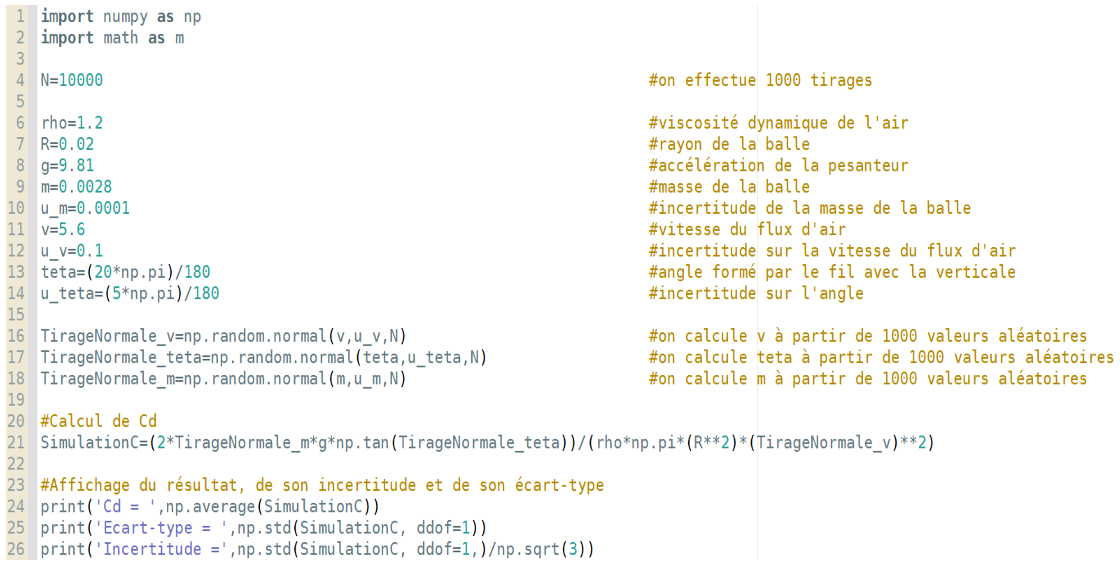
On obtient des résultats en réalisant le calcul pour différentes vitesses de flux d'air et d'angle. On peut utiliser une méthode Monte-Carlo pour obtenir un résultat précis et ses incertitudes.
Mon camarade s'est chargé de déterminer le coefficient de Magnus de la balle
Vérification des valeurs trouvées
Nous avons ensuite voulu vérifier la cohérence des résultats obtenus en étudiant la trajectoire de balles de tennis de table.
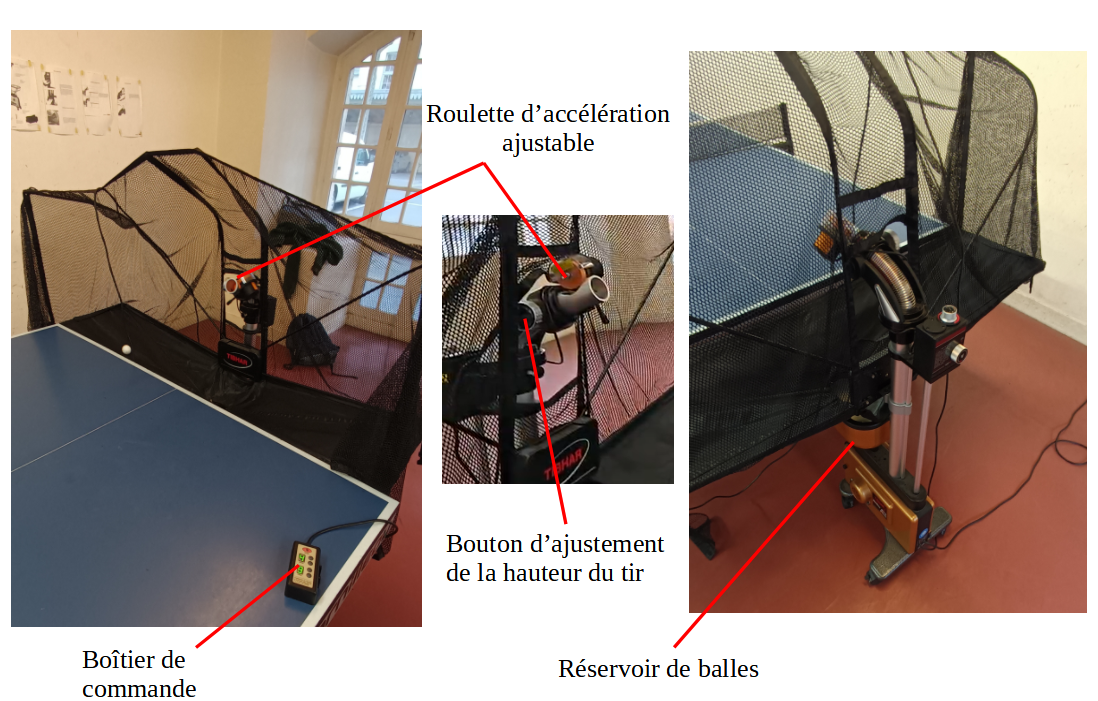
Pour cela nous nous sommes munis d'une machine d'entraînement permettant de lancer des balles à vitesse et effet constants.
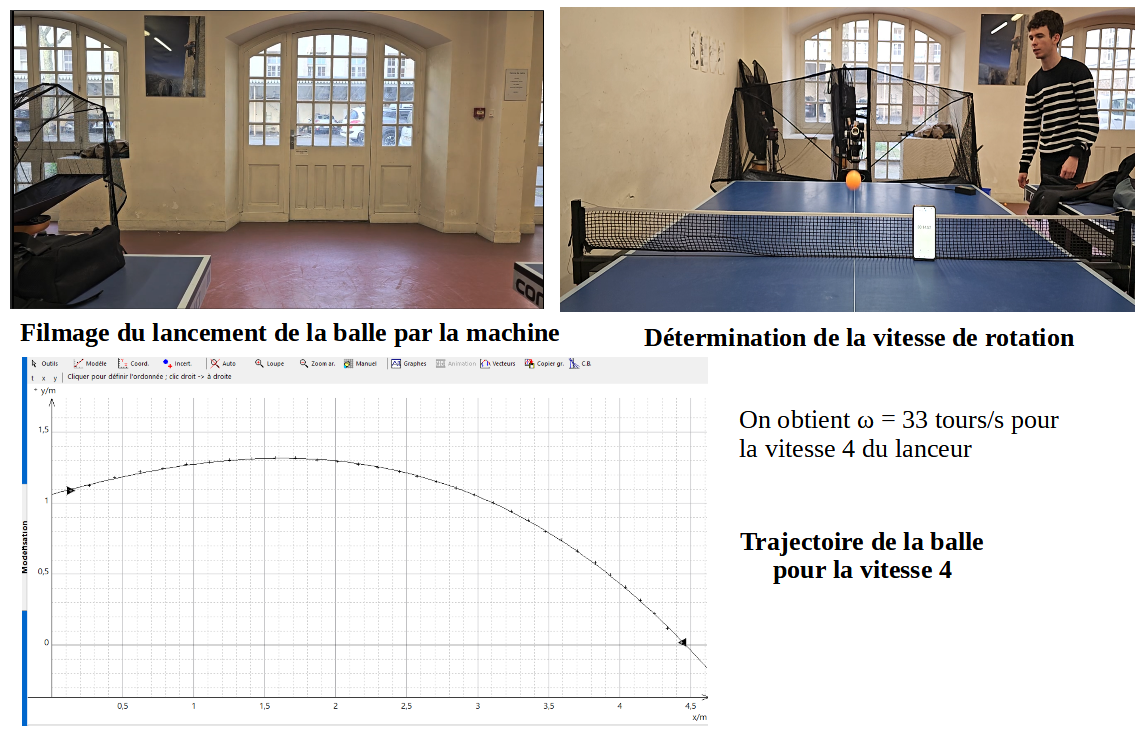
Nous avons filmé la trajectoire de balles lancées par la machine puis nous avons effectué un pointage de cette trajectoire sur Regressi. Nous obtenons alors plusieurs courbes de trajectoires en fonction de la vitesse de rotation de la balle.
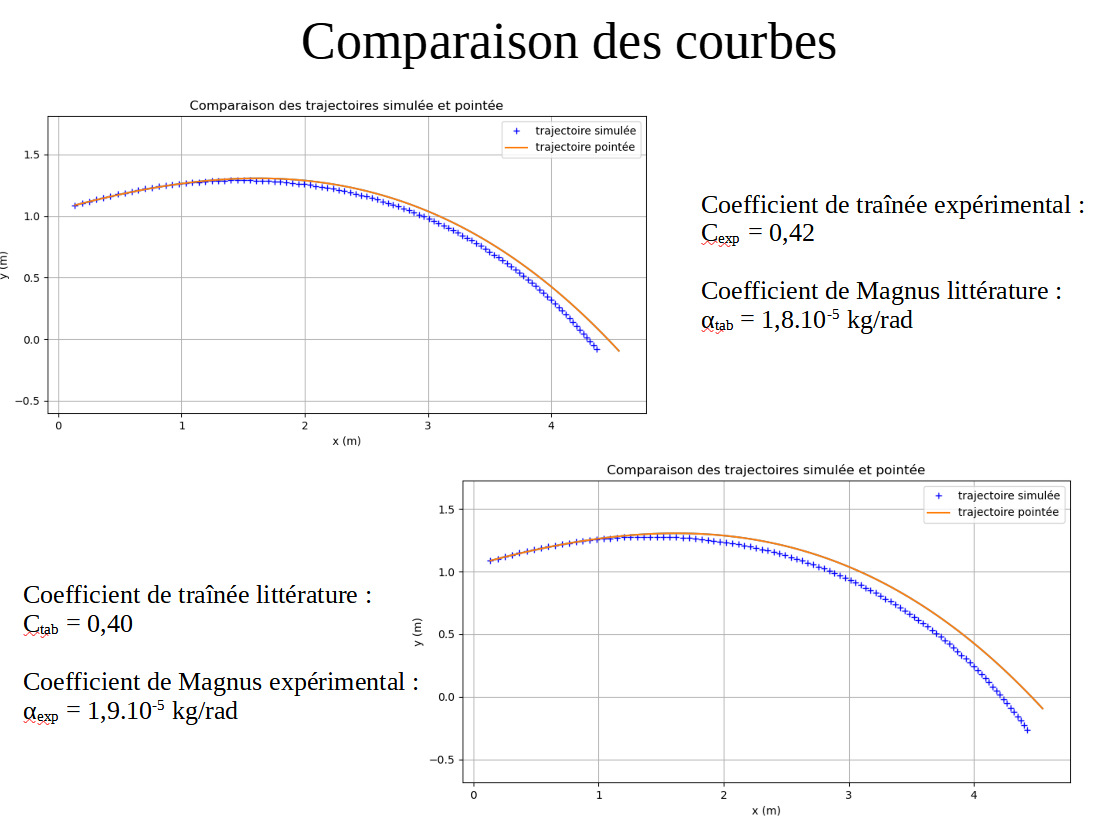
D'autre part, nous avons écrit un programme Python permettant de modéliser la trajectoire théorique de la balle en fonction de la vitesse de lancer et de la vitesse de rotation. Ainsi, nous pouvons comparer la trajectoire de la balle que nous devrions observer avec la valeur des coefficients que nous avons trouvé précédemment, avec la trajectoire filmée de la balle. On observe que ces deux courbes sont assez proches, la trajectoire filmée correspond à la trajectoire modélisée, nos coefficients sont donc satisfaisants.